What is a Linear Equation?

What are linear equations? Linear equations generally will contain an x and y variable in an equation, which contains an equal sign (=). In this equation, you can input an x value and solve for the y value to plot a point on the coordinate plane. The coordinate plane is essentially two number lines, one vertical and one horizontal, that creates a two dimensional space in which points and lines can be graphed. The horizontal axis is the x-axis and the vertical axis is the y-axis. In a linear equation, for any number, x, you can plug it into the equation and solve for y. Then, on the coordinate plane, at the x value and the y value, a point can be plotted. 

For linear equations, the result is a line on a graph, but how do we get a line on the graph? With linear equations, you can choose two x values and solve for y. Then, plot the points on the graph and connect them with a straight line. Now, to get the y value for any x value, you can simply find the x value on the x-axis and then find what the y value is for that x value! 

This may still be confusing, so let’s look at an example:

Linear equation: y = 2x + 1

• x and y are variables. Usually, we plug the x into the equation to solve for y.
  
• 2 is the coefficient for the x variable and also the slope of the line. When we plug x into the equation, the first thing we do is multiply it by 2 for this equation.
  
• 1 is the y-intercept. The y-intercept is the point at which the line crosses through the x axis, which is when x = 0. If x equals 0, then 2 multiplied by x is 0, and then we add 1 to get the y-intercept which is simply the y-value when x is 0.
  

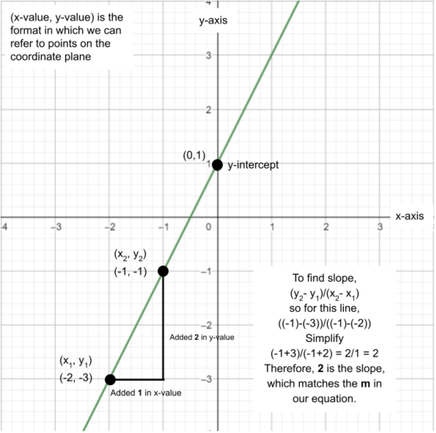
This form is called slope-intercept form. Many other forms of the linear equation exist, but we will focus on just this one. This form can be put as y=mx+b. In this, m is the slope and b is the y-intercept. The x and y are both variables. To calculate slope, find two points in the line by plugging any two x values into the linear equation. In the image, we plugged in -2 and -1 as our two x values. This results in:

y = 2(-2) + 1, so y = -3 → (-2, -3)
y = 2(-1) + 1, so y = -1 → (-1, -1)

Although we know just looking at the equation that the slope of the line is 2, we can also calculate it using the equation (y2- y1)/(x2- x1). Looking at the calculations shown on the image, we know that the slope will be 2. 
Let’s practice! We are given points (1,4) and (3,-2). Find the slope.
Solution:
Let’s make (3,-2) the (x2, y2) and make (1,4) the (x1, y1).
Now we can plug the value into the equation, (y2- y1)/(x2- x1).
Therefore, 
(y2- y1)/(x2- x1) → ((-2) - 4)/(3 - 1) = (-6)/(2) = -3
Slope = -3
Now, we can also find the y-intercept by plugging in a single point and the slope since we know that the slope is m.
y = -3x + b
4 = -3(1)+b
4 = -3 + b (now we will add -3 to each side to solve for b)
7 = b
Therefore, our complete equation for the line containing the points (1,4) and (3,-2) is y=-3x+7.